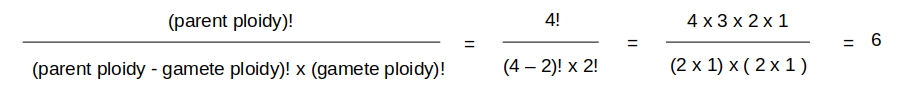Potato: Genetics – The Basics

Last year, I put together a summary of potato color genetics and ever since I have been getting emails asking questions.  A lot of those questions center on how to use the information.  I’m happy to try to answer those questions to the best of my ability, because I think potato genetics are fun.  This is one of those cases, however, where describing what exists is much easier than explaining how to use it.  It will take more than one post to get there, but this post will deal with the application of basic genetics in breeding diploid and tetraploid potatoes.

Basic Concepts

Example Genes

I’m going to use two example genes in this post, both of which I’ve made up:

Sq is a dominant gene that determines the shape of potatoes.  The dominant allele, Sq, makes potatoes square.  The recessive allele, sq, makes potatoes round.

Z is a recessive gene that determines whether or not potatoes have zebra stripes.  The dominant allele, Z, has no stripes.  The recessive allele, z, has zebra stripes.

Phenotype and Genotype

A phenotype is the expression of a gene or combination of genes – it is something that you can see, taste, or otherwise observe in some way, even if it isn’t obvious.  For example, square tubers and zebra striped tubers are phenotypes, as are less obvious things like how much sugar or protein a variety contains or how well it resists a particular pest.

A genotype is the genetic configuration behind a trait.  Here, things get a little more complicated and we have to work in some other ideas.  A genotype is a statement of the alleles of a given gene found in a particular plant.  An allele is a variation of the gene.  Genes don’t necessarily have different alleles, but most do.  Our example genes, Sq and Z, each have two alleles, a dominant allele and a recessive allele.  The convention is to represent dominant alleles starting with capital letters and recessive alleles starting with lowercase letters.  So, Sq and Z are the dominant alleles and sq and z are the recessive alleles.

Dominant and Recessive Genes

A dominant allele creates the trait that it controls whenever it is present in the plant.  We decided above that Sq is a dominant gene, so if any of the alleles carried by a plant is Sq, then the plant makes square tubers.

A recessive allele creates the trait that it controls whenever it is the only allele present in the plant.  We decided above that Z is a recessive gene, so if all of the alleles carried by a plant are z, then the plant makes zebra striped tubers.  If even one of the alleles is Z, though, the tubers will not be striped.

Diploid Genetics

We’re going to do our first examples with diploid potatoes.  Diploid potatoes are not commonly grown, but diploid potato genetics are much easier to understand than tetraploids, so this is a good foundation to build upon.

A diploid potato has two complete sets of chromosomes and, therefore, two copies of each gene.  The alleles can be different or they can be the same.  So, a diploid potato can have the following genotypes for Sq: SqSq, Sqsq, sqSq, or sqsq.  We consider the two middle types to be synonymous – when there are two different alleles, it doesn’t matter which chromosome has each one.  So, the options can be condensed to SqSq, Sqsq, and sqsq.  When both alleles are the same, we call them homozygous.  When the alleles are different, we call them heterozygous.

Diploid Sq Genotypes

Genotype	Zygosity	Dominance	Phenotype	Explanation
SqSq	Homozygous	Dominant	Square	Sq is a dominant gene, so you only need one dominant (uppercase) allele to express the trait.  This genotype has more than one dominant allele, so the potato has the dominant phenotype: tubers are square.
Sqsq	Heterozygous	Dominant	Square	This genotype has one dominant allele and one recessive allele.  As above, you only need one dominant allele to express the dominant trait and this genotype has one.  The tubers are square.
sqsq	Homozygous	Recessive	Round	This genotype has two recessive alleles.  That means that the recessive trait is expressed, so the potato has the recessive phenotype: tubers are round.

Diploid Z genotypes

Genotype	Zygosity	Dominance	Phenotype	Explanation
ZZ	Homozygous	Dominant	Not striped	Z is a recessive gene, so you need two recessive (lowercase) alleles to express the trait.  This genotype does not have two recessive alleles, so the potato has the dominant phenotype: no stripes.
Zz	Heterozygous	Dominant	Not striped	Z is a recessive gene, so you need two recessive (lowercase) alleles to express the trait.  This genotype has only one recessive allele, so the potato has the dominant phenotype: no stripes.
zz	Homozygous	Recessive	Zebra striped	This genotype has two recessive alleles, so it is able to express the recessive phenotype.  The tubers have zebra stripes.

Let’s consider these the two tables above for a moment.  Sq is a dominant gene.  Z is a recessive gene.  What is the difference between these two types of genes?  Sq makes square tubers when dominant.  Z makes zebra striped tubers when recessive.  Could we express these in different ways?  What if we instead described Z as a dominant gene that makes stripeless tubers?  It would still make zebra-striped tubers when homozygous recessive.  It would still make stripeless tubers when a dominant allele is present.  The only thing that has actually changed is the terminology.  The concept of dominant and recessive genes is a convenience for us, but it is conceptual, not real.  Whether the gene is dominant or recessive, when paired, it still produces the same three genotypes: homozygous dominant, heterozygous, and homozygous recessive.  So, dominant and recessive are just different ways of thinking about the same condition.  I am pointing this out because people have a tendency to get the idea that recessive genes are more difficult to understand.  If you understand how dominant genes work, you understand how recessive genes work and vice-versa.  It’s all the same.

Crosses

The point in understanding everything above is to be able to guide your breeding work.  If you know the genotypes of the varieties that you are working with, you can predict the results of crosses between those varieties.  That allows you to develop phenotypes without having to always resort to trial and error.

The essential tool for predicting the results of crosses is the Punnett Square, a staple of high school biology classes.  You have probably been exposed to them at some point, although you will be among the majority if you are sketchy on the details.  That’s OK.  This is a pretty simple concept and you should find it easy to use now that you have a reason to apply it.  A Punnett Square is just a visual representation of the alleles carried in every possible gamete (pollen and ovules) and how they can combine to form zygotes.

Let’s consider a cross between a variety that is homozygous dominant for Z (no stripes) and a variety that is homozygous recessive for Z (zebra striped).  That is a cross of ZZ x zz.  A Punnet Square can be used to show all of the possible outcomes from this cross.  We’ll put ZZ at the top (yes, that’s ZZ top in case you missed it) and zz on the side.  It doesn’t matter which way you do it though.

	Z	Z
z	Zz	Zz
z	Zz	Zz

The outcome here is straightforward.  You don’t even need a 2×2 grid for this cross, since there is only one possible outcome.  All of the progeny will be heterozygous.  When a variety is heterozygous, you get the dominant phenotype, so none of the progeny will be striped.

How about if we cross a variety that is homozygous dominant for Z with a variety that is heterozygous?  This is a cross of ZZ x Zz.

	Z	Z
Z	ZZ	ZZ
z	Zz	Zz

Now we have more than one genotype.  The progeny will be 50% ZZ and 50% Zz, a genotypic ratio of 1:1.  You won’t be able to tell the genotypes apart though, because they have the same phenotype.  Because Z is dominant and they all contain at least one dominant allele, they are all stripeless.

Let’s try another cross between a variety that is heterozygous and a variety that is homozygous recessive.  This is a cross of Zz x zz.

	Z	z
z	Zz	zz
z	Zz	zz

Again, we have two different genotypes in the progeny, but this time we also have two different phenotypes.  This is called segregation.  This cross segregates for two phenotypes: 50% Zz, which is stripeless, and 50% zz, which is striped.  We have a genotypic ratio of 1:1 and a phenotypic ratio of 1:1 as well.

Let’s do one more: a cross of two heterozygous varieties.  This is a cross of Zz x Zz.

	Z	z
Z	ZZ	Zz
z	Zz	zz

This cross segregates for two different phenotypes and three genotypes.  The genotypes ZZ and Zz are stripeless.  The zz genotype is striped.  We have a phenotypic ratio of 3:1 from this cross.

Why do phenotypic ratios matter?  Potatoes don’t come with labels that tell you their genotypes.  If you want to use genetics to direct your breeding, then you first need to figure out the genotypes of the varieties that you are working with.  It is possible to puzzle out genotype from phenotype by making crosses to different varieties and comparing the ratios.  This is called test crossing and we’ll get to that in a future post.

Tetraploid Genetics

Most potatoes are tetraploid and tetraploid potato genetics are much more complicated than the diploid genetics that we just covered.  Instead of two sets of chromosomes, tetraploids have four sets, which means four copies of each gene.  This makes inheritance much more complex.  While a diploid can only have a single heterozygous combination, a tetraploid has three: simplex, duplex, and triplex.

As a result of these additional heterozygous combinations, we need to introduce a new concept: dosage.  Depending on how a gene works, more copies can result in more production of the proteins that the gene controls.  This makes it much more difficult to predict the phenotypes that can be expressed.

To expand on our examples from above, let’s say that Z phenotypes change with dosage but Sq phenotypes do not.  In addition, let’s say that the degree to which Z is expressed is controlled by the ratio of dominant to recessive alleles.  Let’s see what this looks like.

Genotype	Zygosity	Dominance	Phenotype	Explanation
SqSqSqSq	Homozygous (Quadruplex)	Dominant	Square	Although it has twice as many copies, this genotype is homozygous for Sq and behaves just like the diploid: tubers are square.
Sqsqsqsq	Simplex (Heterozygous)	Dominant	Square	Because it has at least one dominant allele, the tubers are square.
SqSqsqsq	Duplex (Heterozygous)	Dominant	Square	Because it has at least one dominant allele, the tubers are square.
SqSqSqsq	Triplex (Heterozygous)	Dominant	Square	Because it has at least one dominant allele, the tubers are square.
sqsqsqsq	Homozygous (Nulliplex)	Recessive	Round	Although it has twice as many copies, this genotype is homozygous for sq and behaves just like the diploid: tubers are round.

In a tetraploid, Sq behaves just like it does in a diploid, but there are twice as many genotypes that produce the square phenotype.  We’ll see the ramifications of this when we do some example crosses below.

Genotype	Zygosity	Dominance	Phenotype	Explanation
ZZZZ	Homozygous (Nulliplex)	Dominant	Not striped	Although it has twice as many copies, this genotype is homozygous for Z and behaves just like the diploid: no stripes.
ZZZz	Simplex (Heterozygous)	Recessive	Not striped	With this gene, the ratio of recessive to dominant must be greater than 1:1 for zebra stripes.  The simplex configuration is 1:3, so the tubers have no stripes.
ZZzz	Duplex (Heterozygous)	Recessive	Not striped	With this gene, the ratio of recessive to dominant must be greater than 1:1 for zebra stripes.  The duplex configuration is 1:1, so the tubers have no stripes.
Zzzz	Triplex (Heterozygous)	Recessive	Lightly striped	With this gene, the ratio of recessive to dominant must be greater than 1:1 for zebra stripes.  The triplex configuration is 3:1, so the tubers have stripes, but they are less pronounced than they are in the full homozygous recessive configuration.  We’ll call this phenotype “lightly striped.”
zzzz	Homozygous (Quadruplex)	Recessive	Normally striped	Although it has twice as many copies, this genotype is homozygous for z and behaves just like the diploid: tubers have zebra stripes.  We’ll now call this phenotype “normally striped.”

With this gene, there are more possible phenotypes in a tetraploid than in a diploid: no stripes, light zebra stripes, and normal zebra stripes.  In addition, there are two more genotypes that correspond to the stripeless phenotype than there are in diploids, so the zebra striped phenotype will be rarer in populations where both alleles are present.

Crosses

There is nothing better than lots of examples to learn genetics, so let’s do some more Punnett Squares.  If you thought that diploid Punnett Squares were fun, you are going to love tetraploids.

We’ll do the same types of crosses that we did for diploids so that you can compare.  Where we only did examples with Z above, we’ll do both Z and Sq in this section because they function differently in tetraploids.  Let’s start with the cross of a homozygous dominant with a homozygous recessive.  These crosses are ZZZZ x zzzz and SqSqSqSq x sqsqsqsq.  The first thing that we need to do is to figure out what the possible gametes are to set up the Punnett Square.  We didn’t need to to this before because the gametes could only contain one allele.  Now they can contain two alleles, randomly paired from the four total alleles.  It is still easy for this cross, since there is only one possible allele for each variety:

	ZZ
zz	ZZzz

 

	SqSq
sqsq	SqSqsqsq

Yep, that’s it.  All of the tubers in the Z example will be stripeless and all of the tubers in the Sq example will be square.  That was an easy one, but it is a special case.  The rest will take some more work.

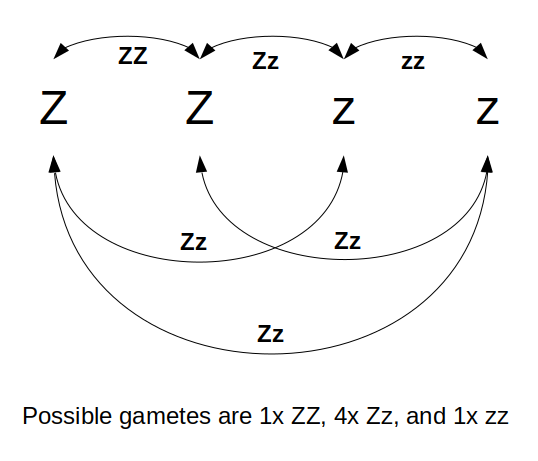
Barring the special, homozygous cases above, constructing Punnett Squares for tetraploids requires a bit more thought than it does for diploids.  In diploids, there are only two possible types of gametes, but in tetraploids, there are usually six.  You must determine the genotypes of each of these six gametes by identifying all the possible pairings of the four alleles in the variety.  The easiest way to do this is with a gamete pairing diagram.  Write out the four alleles and then draw arrows connecting each allele to every other allele.  The genotypes of each possible gamete are the two alleles connected by the arrow.

Let’s do a cross between a homozygous dominant and an equally heterozygous (duplex) variety.  These crosses will be ZZZZ x ZZzz and SqSqSqSq x SqSqsqsq.  The homozygous varieties are easy, just like the examples above.  They can only product gametes with a ZZ or SqSq genotype.  The heterozygous varieties are trickier, so we will find them with a gamete pairing diagram:

You can also solve for the number of different gametes mathematically.  You will still need to figure out what the pairings are, but you can use this to double check that you came up with the right number.  We’ve already established that the answer is six in this case, but if you were to work with varieties of a ploidy that we haven’t discussed (hexaploid, for example), you might want to know how to figure it out on your own.

To boil this down, when constructing Punnett Squares for tetraploid potatoes, homozygous varieties have only one possible gamete genotype, so you only need one row or column for them.  For heterozygous varieties, you will always need six rows or columns, even if many of the gametes have the same genotype, because that preserves the correct genotypic and phenotypic ratios in your results.

The four chromosomes of the parent can produce six different pairings in a gamete.  Four of them are identical (Zz), but you need to include all four in order to get accurate ratios of genotypes and phenotypes.  So, the simplest Punnett Square looks like this:

	ZZ	Zz	Zz	Zz	Zz	zz
ZZ	ZZZZ	ZZZz	ZZZz	ZZZz	ZZZz	ZZzz

We get 1 ZZZZ, 4 ZZZz, and 1 ZZzz.  All of the progeny are stripeless.

	SqSq	Sqsq	Sqsq	Sqsq	Sqsq	sqsq
SqSq	SqSqSqSq	SqSqSqsq	SqSqSqsq	SqSqSqsq	SqSqSqsq	SqSqsqsq

We get 1 SqSqSqSq, 4 SqSqSqsq, and 1 SqSqsqsq.  All of the progeny are square.

Now let’s do the heterozygous duplex variety crossed with a homozygous recessive variety.  This will be a cross of ZZzz x zzzz.  It works exactly the same way:

	ZZ	Zz	Zz	Zz	Zz	zz
zz	ZZzz	Zzzz	Zzzz	Zzzz	Zzzz	zzzz

We get 1 ZZzz, 4 Zzzz, and 1 zzzz.  That is 1 stripeless, 4 lightly striped, and 1 normally striped.

	SqSq	Sqsq	Sqsq	Sqsq	Sqsq	sqsq
sqsq	SqSqsqsq	Sqsqsqsq	Sqsqsqsq	Sqsqsqsq	Sqsqsqsq	sqsqsqsq

We get 1 SqSqsqsq, 4 Sqsqsqsq, and 1 sqsqsqsq.  That is 5 square and 1 round.

Finally, let’s do a duplex heterozygote crossed with a duplex heterozygote.  I’m going to skip Sq this time.  This will be a cross of ZZzz x ZZzz.  This is a fun one:

	ZZ	Zz	Zz	Zz	Zz	zz
ZZ	ZZZZ	ZZZz	ZZZz	ZZZz	ZZZz	ZZzz
Zz	ZZZz	ZZzz	ZZzz	ZZzz	ZZzz	Zzzz
Zz	ZZZz	ZZzz	ZZzz	ZZzz	ZZzz	Zzzz
Zz	ZZZz	ZZzz	ZZzz	ZZzz	ZZzz	Zzzz
Zz	ZZZz	ZZzz	ZZzz	ZZzz	ZZzz	Zzzz
zz	ZZzz	Zzzz	Zzzz	Zzzz	Zzzz	zzzz

Wow!  Check that out.  One thing that you can see right away is that homozygous configurations are a lot less likely than they were in diploids.

This cross yields 1 ZZZZ, 1 zzzz, 8 ZZZz, 8 Zzzz, and 18 ZZzz.  As we discussed above, ZZZZ, ZZZz, and ZZzz have no stripes, Zzzz has light stripes, and zzzz has normal stripes.  So this cross produces 27 stripeless, 8 lightly striped, and 1 normally striped plant.  In the diploid example with the same ratio of alleles (Zz x Zz), there was a 25% chance of getting a normally striped plant, but in the tetraploid, there is only a 2.8% chance.  On the other hand, in the diploid, there was no chance of getting any lightly striped progeny, but in the tetraploid, there is a 22% chance.

When breeding, you generally want to produce varieties that are homozygous for important traits so that you can use them predictably to make crosses.  As you can see, that is a lot easier with diploids than tetraploids.  It takes a much larger number of plants to obtain homozygous varieties.  And we are only considering individual genes here.  Imagine if you needed to produce a variety that was homozygous for 20 different genes, all with inheritance this complex.  You might try that with a diploid, but with a tetraploid, you would probably decide to focus on a much smaller number of genes.  I’ll delve into the math on this subject a little bit next time.

That’s probably enough potato genetics for one sitting.  In the next part, in a week or two (optimistically), I will also introduce the concepts of linkage, codominance, incomplete dominance, multiallelic loci, epistasis, and disomic segregation in tetraploids.  After that, maybe we will get into test crosses.

If you made it this far, you would probably enjoy our other articles on potato breeding.